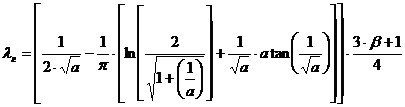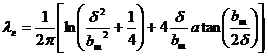|
|
Применение полевых методов в электромагнитных расчетах электрических машинЧасть 2РЕШЕНИЕ НЕКОТОРЫХ ПРАКТИЧЕСКИХ ЗАДАЧ ЭЛЕКТРОМАГНИТНОГО РАСЧЕТА ЭЛЕКТРИЧЕСКИХ МАШИН2.1. Расчет проводимости пазового рассеяния при наличии магнитных клиньевОграничимся здесь рассмотрением только тех пазов, в которых силовые линии потока пазового рассеяния, проходящие через клин, не проходят в то же время через часть паза, занятую проводниками с током. Другими словами, рассмотрим ту часть пазового рассеяния, которую обычно называют рассеянием через верхнюю часть паза, предполагая при этом, что все линии этого потока сцеплены со всеми проводниками паза. Заметим, что проводимость пазового рассеяния для части паза, занятой проводниками с током, также может быть найдена с помощью конечно-элементной модели. В этом случае необходимо определить средневзвешенное на токовом участке паза значение векторного магнитного потенциала. Операция по определению этого значения обычно входит в число функций постпроцессора конечно-элементной программы. В современной научно-технической литературе, посвященной расчету параметров электрических машин, проводимость верхней части паза обычно рассматривается с учетом т. наз. рассеяния по коронкам (головкам) зубцов. Для коэффициента проводимости λг в [2-1] рекомендуется формула, полученная в результате решения полевой задачи для области паза без тока методом конформных преобразований (задача Картера):
где a = (bш/2δ)2 , bш - раскрытие паза, δ - зазор (приведенный, с учетом зубчатости противоположного сердечника), β – относительный шаг обмотки (далее принят равным единице). В [2-2] приводится формула для коэффициента проводимости по коронкам зубцов, по форме отличающаяся от (2.1), но полученная тем же методом и дающая те же результаты:
Рассчитанная по (2.1) или (2.2) проводимость по коронкам зубцов должна быть добавлена к проводимости шлицевой и клиновой части паза, однако вполне точные результаты получаются только в том случае, если поле рассеяния в этой зоне при удалении от зазора успевает выровняться (в картине поля рассеяния при этом появляются прямые силовые линии, перпендикулярные оси паза).
В качестве примера
рассмотрим рассеяние в верхней части паза при
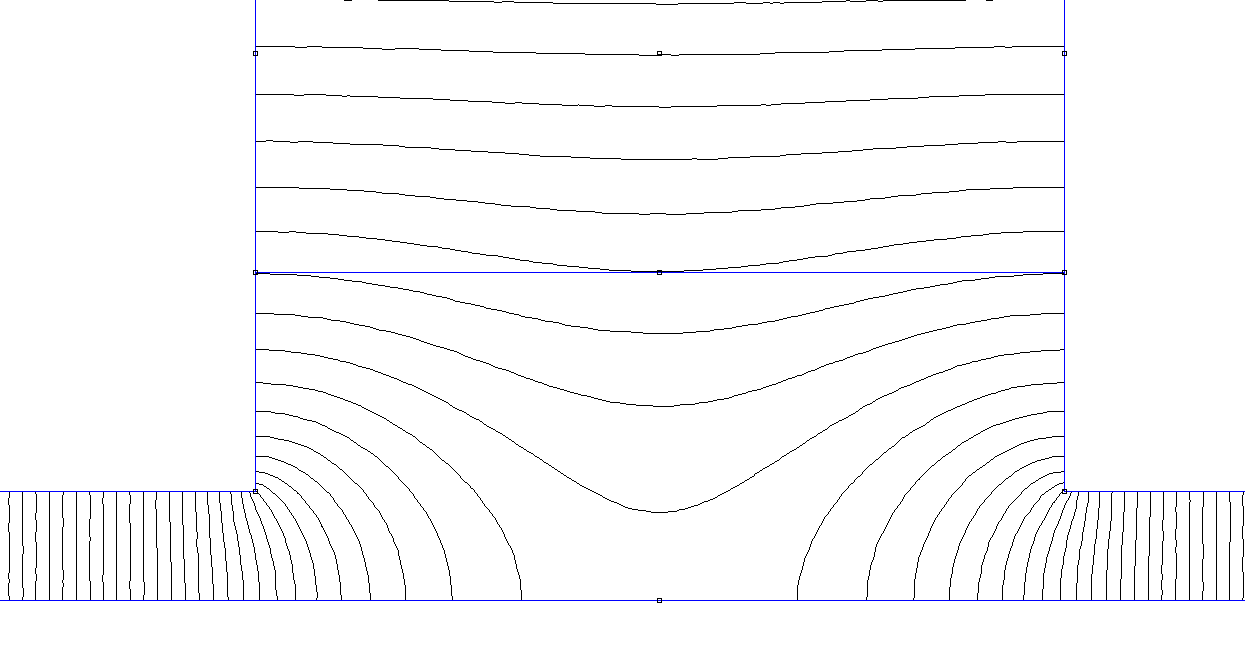
Рис. 2.1. Картина поля в верхней части паза при bш = 3,7 мм и δ = 0,5 мм. Точка А1 углублена в паз на 1 мм, точка А2 - на 2 мм.
Расчетное значение
коэффициента проводимости рассеяния по коронкам зубцов при заданных размерах
оказывается равным - 0,097. Коэффициент проводимости для участка верхней части
паза, ограниченного силовыми линиями, проходящими через точки А0
и А1 , найденный по результатам моделирования, равен 0,200, в
то время как расчетное значение его равно 0,173 Имея в виду замечание, сделанное относительно картины поля в верхней части паза, можно сделать вывод о том, что нецелесообразно разделять магнитную проводимость этой зоны на отдельные составляющие, в особенности, если рассматривается (и моделируется) паз с заданными размерами. Оценивая точность применяемых на практике расчетных формул и влияние на проводимость пазового рассеяния магнитных клиньев, следует определять полный поток рассеяния в верхней части паза. Этот поток находится по разности значений векторного магнитного потенциала в точках А0 и А1, показанных на рис. 2.1. В качестве примера рассмотрим проводимость рассеяния верхней части паза асинхронного двигателя мощностью 15 кВт (из примера расчета в [2-3]. Размеры паза даны на рис. 2.2. При расчете по обычно используемым при проектировании формулам значение коэффициента проводимости рассеяния в верхней части паза получается равным 0,524. По результатам моделирования (по разности векторных магнитных потенциалов точек А0 и А1, показанных на рис. 2.1) коэффициент проводимости получается равным 0,528.
|