|
|
Применение полевых методов в электромагнитных расчетах электрических машин1.3.3. Определение коэффициентов ξd, ξq, и kqd, по методике Р.РихтераПо результатам опыта III найдены амплитуды продольной и поперечной составляющих индукции Вδd1mIII и Вδq1mIII (умножением амплитуды Вδ1mIII на cos(29,9o - 7,43o) и на sin(29,9o - 7,43o) соответственно): Вδd1mIII = 0,968 Т и Вδq1mIII = 0,400 Т. Сравнивая индукции Вδd1mIII и Вδd1mII, убеждаемся, что поперечная реакция якоря оказывает дополнительное размагничивающее действие по продольной оси благодаря насыщению стали статора. Для определения коэффициентов ξd , ξq и kqd воспользуемся значениями коэффициентов формы поля и реакции якоря, принятыми для гидрогенератора в примере расчета в [1-5] : kf = 1,082, kd =0,890, kq = 0,578, kad =0,823, kaq = 0,534. Заметим, что эти значения хорошо совпадают с найденными с помощью конечно-элементных моделей для ненасыщенного генератора (1,084, 0,907, 0,593, 0,837 и 0,547 соответственно). Эквивалентные МДС Fadm.нас, Faqm.нас и Fqdm , найденные по амплитудам основных гармоник индукции и частичной характеристике холостого хода, равны 10400 А, 6600 А и 1700 А соответственно. Найденные таким образом эквивалентные МДС позволяют определить искомые коэффициенты насыщения: ξd = 0,97 , ξq = 0,95 , kqd = 0,006. Для того чтобы сравнить значения коэффициентов ξd , ξq и kqd, найденных описанным способом по результатам моделирования, с определенными по графическим зависимостям в [1-4, гл 55], необходимо определить коэффициент насыщения kza = Ff1/Fδ для результирующего поля. Поскольку результирующее поле несимметрично, можно предложить по крайней мере два способа определения этого коэффициента: по средним значениям магнитных напряжений зубцов и зазора вблизи краев полюса и по средней силовой линии поля. Найденный вторым способом коэффициент kza равен 1,16. Этому значению по графикам в [1-4, гл 55] соответствуют коэффициенты насыщения ξd = 0,97 , ξq = 0,73 , kqd = 0,003, что довольно близко к значениям, найденным по результатам моделирования. Частичная характеристика холостого хода может быть определена и на модели, в которой воспроизводятся реальные свойства стали ротора. В таблице 1.9 представлены данные, полученные на такой модели. Как показывает сравнение двух характеристик, для выбранного соотношения размеров, при котором сердечник полюса оказывается насыщенным примерно в той же мере, что и зубцовая зона статора, расхождение между характеристиками в области сильного насыщения может быть заметным. Таблица 1.9
Примечание. магнитные напряжения измерялись вдоль средней силовой линии. В заключение заметим, что описанный способ учета насыщения с помощью коэффициентов ξd , ξq и kqd , как на это и указывается в [1-4, гл 55], является приближенным и используется при приближенном расчете тока возбуждения в режиме нагрузки с учетом насыщения магнитной цепи. Достоинством этого способа является то, что решение (данные режима) может быть получено довольно быстро. В том случае, если требуется уточнить полученное приближенное решение, можно прибегнуть к моделированию режима нагрузки на конечно-элементной модели поперечного сечения (более подробно об этом будет сказано в гл. 3).
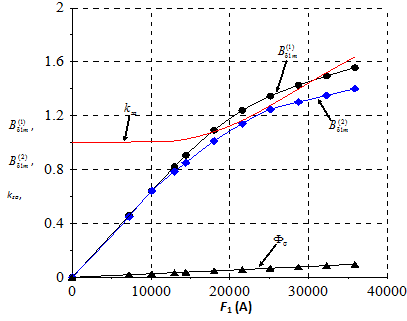
Рис. 1.26. Частичные характеристики холостого хода
Частичная характеристика холостого хода, определенная иным образом – при воспроизведении нелинейных свойств стали полюсов ротора и статора. Из сравнения данных, приведенных в двух таблицах, видно, что вид частичной характеристики холостого хода мало зависит от способа ее определения.
|