|
|
Применение полевых методов в электромагнитных расчетах электрических машин1.1. Определение обмоточных коэффициентовНесмотря на необходимость дополнительной операции – гармонического анализа – определение kоν вторым способом оказывается проще, поэтому в дальнейшем будем рассматривать модели второго типа. На рис. 1.5 показана такая модель для трехфазной двухполюсной машины с q, равным двум. Вначале, при оценке точности модели, относительная магнитная проницаемость сердечников была принята равной 104, раскрытия пазов и зазор достаточно малы по сравнению с полюсным делением, а второй сердечник был принят гладким. При этих условиях точность определения обмоточных коэффициентов по модели рис. 1.5, столь же высока, как и по рассмотренным выше моделям. В модели, показанной на рис. 1.5, поле создается только одной катушкой с диаметральным шагом. Распределение поля вдоль контура, проведенного посередине зазора, в этом случае представляет собой прямоугольную трапецию. Гармонический анализ этого распределения может быть выполнен с помощью встроенной функции fft пакета MathCAD (быстрое преобразование Фурье – fast Fourier transform). С этой целью в MathCAD’овский файл должны быть переданы в виде текстового файла 2N (N – целое число) значений нормальной составляющей индукции, взятые на контуре, проведенном в зазоре. Несмотря на необходимость дополнительной операции – гармонического анализа – определение kоν вторым способом оказывается проще, поэтому в дальнейшем будем рассматривать модели второго типа. На рис. 1.5 показана такая модель для трехфазной двухполюсной машины с q, равным двум. Вначале, при оценке точности модели, относительная магнитная проницаемость сердечников была принята равной 104, раскрытия пазов и зазор достаточно малы по сравнению с полюсным делением, а второй сердечник был принят гладким. При этих условиях точность определения обмоточных коэффициентов по модели рис. 1.5, столь же высока, как и по рассмотренным выше моделям. В модели, показанной на рис. 1.5, поле создается только одной катушкой с диаметральным шагом. Распределение поля вдоль контура, проведенного посередине зазора, в этом случае представляет собой прямоугольную трапецию. Гармонический анализ этого распределения может быть выполнен с помощью встроенной функции fft пакета MathCAD (быстрое преобразование Фурье – fast Fourier transform). С этой целью в MathCAD’овский файл должны быть переданы в виде текстового файла 2N (N – целое число) значений нормальной составляющей индукции, взятые на контуре, проведенном в зазоре.
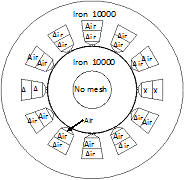
Рис. 1.5. Конечно-элементная модель для определения обмоточных
Для определения обмоточных коэффициентов необходимо воспроизвести на модели реальную обмотку – с заданным распределением по пазам и укорочением шага, выполнить гармонический анализ поля в зазоре и взять отношения амплитуд гармоник индукции поля реальной обмотки и поля катушки с диаметральным шагом. Ток фазы при этом надо сохранить. В табл. 1.1 приведены результаты определения обмоточных коэффициентов на основе модели по рис. 1.5 при указанных идеализированных условиях. После того, как было смоделировано поле сосредоточенной обмотки с диаметральным шагом, на участках соответствующих пазов были заданы плотности тока, воспроизводящие мгновенные значения токов катушек распределенной обмотки с укороченным шагом. Значения плотностей тока были подобраны таким образом, чтобы индукции в магнитопроводе были реальными (индукция в ярме статора Ba1 = 1,18 Т, в ярме ротора Ba2 = 1,15 Т, в зубце статора Bz1 = 1,46 Т). Как видно из табл. 1.1, результаты моделирования с достаточно высокой точностью совпадают с расчетом по аналитическим выражениям и, таким образом, подобного рода модели могут быть использованы для оценки допущений, принятых при выводе этих выражений. Таблица 1.1
В таблице 1.2. приведены результаты определения обмоточных коэффициентов на конечно-элементной модели при тех же условиях, что и раньше, за исключением того, что для сердечников был применен материал с нелинейной кривой намагничивания (сталь 1512). Даже для наиболее выраженных зубцовых гармоник расхождение между «опытными» (полученными на модели) и расчетными значениями обмоточного коэффициента может в этом случае превышать 5%. Для гармоник с меньшей амплитудой это расхождение может составлять десятки процентов. Заметим, что в обычной расчетной практике влияние насыщения стали учитывается интегрально - введением коэффициента насыщения, в равной мере изменяющего амплитуды всех гармоник.
|