1.2.
Основные уравнения магнитной
гидродинамики и
определяющие критерии подобия МГД–потоков
Следует условиться, что мы будем рассматривать проводящие жидкости как сплошную
среду немагнитную с магнитной проницаемостью
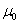 .
Поэтому следует считать, что проводимость жидкости, обусловленная свободными
зарядами (ионами или электронами), воздействует на магнитное поле возбуждения
электрическими токами текущими в ней. В свою очередь токи проводимости вызывают
при взаимодействии с магнитным полем электромагнитную объемную силу .
Поэтому следует считать, что проводимость жидкости, обусловленная свободными
зарядами (ионами или электронами), воздействует на магнитное поле возбуждения
электрическими токами текущими в ней. В свою очередь токи проводимости вызывают
при взаимодействии с магнитным полем электромагнитную объемную силу
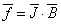 .
Магнитостатическими силами и электростатическими силами обычно пренебрегают, как
чрезвычайно малыми по сравнению с силой f.
Относительно большая величина электропроводности жидкостей позволяет в
прикладной магнитной гидродинамике пренебречь токами смещения и конвекции. .
Магнитостатическими силами и электростатическими силами обычно пренебрегают, как
чрезвычайно малыми по сравнению с силой f.
Относительно большая величина электропроводности жидкостей позволяет в
прикладной магнитной гидродинамике пренебречь токами смещения и конвекции.
Теперь совместная
система уравнений гидро– и электродинамики позволяет дать описание
магнитогидродинамических процессов.
Основным
уравнением вязкой несжимаемой жидкости является уравнение Навье–Стокса:
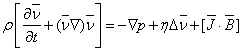 ;
(1.1) ;
(1.1)
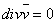 ,
(1.2) ,
(1.2)
где р –
давление в жидкости.
В уравнение
входит пондеромоторная сила 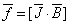 и
локальная скорость в проводящей жидкости и
локальная скорость в проводящей жидкости
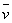 .
Так как рассматриваются «нерелятивистские» скорости течения, то для изотропных
сред уравнения электродинамики записываются в виде: .
Так как рассматриваются «нерелятивистские» скорости течения, то для изотропных
сред уравнения электродинамики записываются в виде:
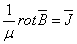 ;
(1.3) ;
(1.3)
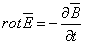 ;
(1.4) ;
(1.4)
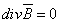 ; (1.5) ; (1.5)
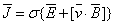 .
(1.6) .
(1.6)
При
последовательном исключении J и Е
из уравнений получаем уравнение индукции
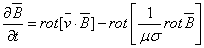 или или
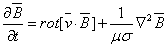 .
(1.7) .
(1.7)
В общем случае
уравнения гидродинамики должны быть дополнены полным уравнением энергии, так как
под действием электромагнитного поля в жидкости имеет место джоулева диссипация
энергии, т.е. выделение тепла. Однако этот сложный процесс обычно в прикладных
задачах не рассматривается. Считается так же, что скорость жидкости значительно
меньше скорости распространения звука в ней. Это позволяет считать жидкость
несжимаемой. Для большинства жидких металлов (калий, натрий, олово, ртуть,
свинец) и соляных растворов (соляная кислота, морская вода) скорость звука слабо
зависит от интенсивности магнитного поля (влияние электрического поля не
обнаружено) и составляет примерно 1450÷2400 м/с.
Анализ полных
уравнений магнитной гидродинамики является очень сложным и в большинстве случаев
аналитически неразрешимым. Поэтому для установления особенностей проявления
магнитогидродинамических эффектов в тех или иных случаях вводятся безразмерные
комплексы или критерии подобия.
Вводя
относительные величины для 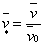 ; ;
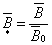 ; ;
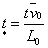 ; ;
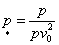 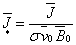 ;
и
т.д., где ;
и
т.д., где 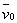 , ,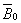 , ,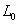 –
некоторые характерные скорость, индукция, линейный размер. –
некоторые характерные скорость, индукция, линейный размер.
Уравнение
Навье–Стокса в безразмерном виде приобретает вид
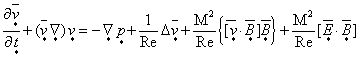 .
(1.8) .
(1.8)
Уравнения
электродинамики записываются также в виде:
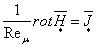 ;
(1.10) ;
(1.10)
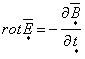 ; (1.11) ; (1.11)
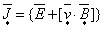 ;
(1.12) ;
(1.12)
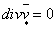 ; (1.13) ; (1.13)
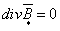 ;
(1.14) ;
(1.14)
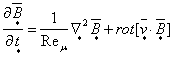 .
(1.15) .
(1.15)
Теперь
непосредственно следует, что магнитогидродинамические явления в потоках
характеризуются тремя основными критериями – Re,
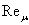 ,
М. ,
М.
Здесь
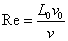 –
число Рейнольдса –
число Рейнольдса
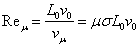 –
магнитное число Рейнольдса, –
магнитное число Рейнольдса,
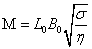 –
число Гартмана, –
число Гартмана,
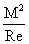 –
число Стюарта –
число Стюарта
Конечно
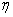 –
динамическая вязкость, v – кинематическая
вязкость –
динамическая вязкость, v – кинематическая
вязкость 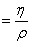 , ,
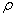 –
плотность. –
плотность.
|